4004. Есть ли цикл?
Дан ориентированный граф.
Определите, содержит ли он цикл.
Вход. Первая
строка содержит одно целое число – количество вершин n (n ≤
50).
Далее следуют n строк по n
чисел в каждой – матрица смежности графа. Каждое число
равно 0 или 1. j-е число в i-й строке
равно 1 тогда и только тогда, когда существует ребро, идущее из
вершины i в вершину j.
Гарантируется, что на главной
диагонали матрицы стоят нули.
Выход. Выведите 0,
если в графе нет циклов, и 1, если хотя бы один цикл существует.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 0 1 1 0 0 1 0 0 0 |
0 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 0 1 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 1 1 0 0 0 0 |
1 |
РЕШЕНИЕ
поиск в
глубину
Анализ алгоритма
Запустим поиск в глубину
на ориентированном графе, рассматривая его как несвязный. Для этого будем
использовать массив used, в котором хранятся цвета вершин графа:
·
used[v] = 0 – вершина v белая, еще не посещена;
·
used[v] = 1 – вершина v серая, в неё уже вошли, но обработка потомков ещё не завершена;
·
used[v] = 2 – вершина v черная, она и все ее потомки полностью обработаны.
Цикл в
ориентированном графе существует, если при поиске в глубину обнаружено ребро, ведущее в серую вершину.
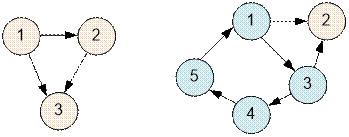
Пример
Примеры графов,
приведённые в условии задачи, имеют следующий вид:
Реализация алгоритма
Объявим матрицу
смежности g и массив состояний
вершин used.
#define MAX 51
int g[MAX][MAX],
used[MAX];
Функция dfs выполняет обход графа в глубину,
начиная с вершины v.
void dfs(int v)
{
Помечаем вершину v как серую, мы
вошли в нее.
used[v] =
1;
Перебираем все вершины, в которые можно попасть из вершины v.
for (int i =
1; i <= n; i++)
Из v в i существует ребро, если g[v][i] = 1.
if (g[v][i])
{
Если вершина i серая, то в
поиске в глубину мы вошли в серую вершину – найден цикл.
if
(used[i] == 1) flag = 1;
Если вершина i белая, то она
еще не посещена. Продолжаем поиск в глубину из нее.
else if
(used[i] == 0) dfs(i);
Если вершина i черная, то
ничего не делаем.
}
По завершении обработки всех сыновей вершины v, помечаем её как
чёрную.
used[v] =
2;
}
Основная часть программы. Читаем матрицу смежности.
scanf("%d", &n);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
scanf("%d",
&g[i][j]);
Запускаем поиск в глубину на ориентированном графе (как на
несвязном).
flag = 0;
for (i = 1; i <= n; i++)
if
(used[i] == 0) dfs(i);
Выводим ответ.
printf("%d\n",
flag);
Java реализация
import java.util.*;
public class Main
{
static int g[][],
used[];
static int n, flag;
static void dfs(int v)
{
//
mark vertex v as GRAY, make an entrance to v
used[v] =
1;
//
we try to go from v to i, i = 1,2,...,n
for (int i = 1;
i <= n; i++)
//
if there exists an edge from v to i
if (g[v][i] ==
1)
{
//
if vertex i is GRAY, we meet cycle
if (used[i] ==
1) flag = 1;
//
if vertex i is not visited, run dfs from there
else if (used[i] ==
0) dfs(i);
//
if vertex i is black (used[i] = 2), do nothing
}
//
mark vertex v as BLACK, make an exit from v
used[v] =
2;
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
g = new int[n+1][n+1];
used = new int[n+1];
for(int i = 1;
i <= n; i++)
for(int j = 1;
j <= n; j++)
g[i][j] = con.nextInt();
flag = 0;
//
run dfs on directed graph like on disconnected graph
for (int i = 1;
i <= n; i++)
if (used[i] ==
0) dfs(i);
System.out.println(flag);
}
}